[강화학습] Reward & Hyperparameter Tuning

• https://essay.utwente.nl/103170/1/Six_Dijkstra_MA_ET.pdf
  • power reward + CRAH setpoint reward, serer outlet temperature penalty + action fluctuation penalty = reward

Reward function

$$r_{t_{i}} = r_{P}(P_{t_{i}}^{HVAC}) \ + \ \lambda_{T_{SP}^{AL_{1}}} \cdot r_{T}(T_{t_{i}}^{AL_{1}}) + \lambda_{T_{constr}^{AL_{2}}} \ \cdot \ p_{T}(T_{t_{i}}^{AL_{2}}) + \lambda_{a} \ \cdot \ p_{a}(\Delta a_{t_{i}}) $$

• $$r_{t_{i}}$$ : total reward at thime $t_i$
• $r_P$ : reward related to power. HVAC power at time $t_i$
• $\lambda_{T_{SP}^{AL1}}$ : scaling factor. related to the setpoint temperature of the CRAH
• $r_T$ : meeting temperature setpoint for the air leaving the CRAH at time $t_i$
• $\lambda_{T_{constr}^{AL2}}$ : scaling factor, penalty on violating the server outlet temperature constraint
• $p_T$ : penalty for violatin gserver outlet tmp, air temperature after the server at time $t_i$
• $\lambda_a$ : vector containing scaling factors, penalty on fluctuations of the each action
• $\Delta a_{t_i}$ : difference between action
• $p_a$ : vector of penaltieson fluctuations of the actions
• HVAC power reward
  $$r_{P}(P_{t_{i}}^{HVAC}) = 1 - \frac{p_{t_{i}}^{HVAC}}{p_{max}^{HVAC}}$$

헉 놀랍게도 제가 한 방식이랑 거의 비슷하네요...

• CRAH setpoint reward
  • leaving air temperature setpoint(Gaussian reward)
    $$ r_{T} = e^{-\frac{1}{2}(\frac{T^{AL1}-T_{SP}^{AL1}}{\sigma_{SP}})^2}$$
  • $\sigma_{SP}$ : 튜닝 가능한 파라미터
  • $T^{AL1}$ : air temperature before server
  • $T^{AL2}$ : air temperature after server
    

• 이쪽에서도 temperature로 인한 reward가 너무 커지지 않게 제한하는 방식을 사용함(TRPO처럼)
  $$T^{AL2} \leq T_{constr}^{AL2}$$

RL Algorithm,

• 오메? 진짜 PPO 씀
• continuous state space
• continuous action space
• stable learning
• model free
• actor critic

RL Tuning

1. hyperparameter tuning
2. reward tuning

하이퍼 파라미터와 보상함수가 서로 영향을 미친다는 사실이 중요함
그르므로 튜닝을 위한 실험을 나눠서 진행하는 것이 agent의 최고 성능으로 바로 이어지지는 않음

• 그러나 보상의 매개 변수를 바꾸면 보상의 정의에 따라 총 보상을 직접 비교하기가 어려워지고, 하이퍼파라미터의 튜닝 실험은 조정해야할 매개변수가 많아질수록 계산 비용이 기하급수적으로 올라감. 따라서 분리해서 하면 시간 소모가 줄어듬
• 또한 환경이 극적으로 변화하지 않았기 때문에 다른 보상함수를 사용하더라도 비슷한 매개변수가 최상의 결과를 가져올 것

Hyperparameter Tuning

• 하이퍼 파라미터 튜닝은 ML 알고리즘의 성능 향상을 위해 쓰이는 흔한 선택임. learning rate나 네트워크 구조를 바꾸는 것이 일반적
• 그러나 RL 알고리즘에서는 하이퍼 파라미터 튜닝이 그렇게 흔한 방법은 아님. 왜냐하면 환경이 다이나믹하기 때문에 더 도전에 가까운 일이 되기 때문...
• 최신 연구에서는 하이퍼 파라미터 튜닝을 수행하는 것이 인상적으로 성능을 향상된다고 말함

하이퍼 파라미터 튜닝을 위해 선택해야할 것들

1. 무슨 파라미터를 튜닝할 것인가
2. 튜닝할 범위는 어떻게 되는가
3. 매개변수 구성을 위해 어떤 샘플러를 사용할 것인가

Hyperparameter selection

• PPO에서는 네트워크 아키텍처 부분에서 사용되는 layer와 노드 개수

Sampler selection

• 하이퍼 파라미터 튜닝에는 계산 비용이 많이 드므로 효과적인 샘플러를 찾는 것이 중요함
• 이 논문에서는 Tree-structured Parzen Estimator sampler를 사용함(TPE)
• Bayesian Sampler의 일종임. 큰 하이퍼 파라미터 공간에 유용하고 pseudo-random samplers의 시스템 탐색에 이점을 가지고 있고, 중간 결과에도 적용할 수 있음

Experiment outline

• Energy plus 환경에서 10개의 episode가 진행될 때마다 서로 다른 hyperparameter 설정을 사용함
• 그리고 training controller가 validation을 진행하고 성능을 비교

Reward Tuning

• reward tuning은 최적화 문제이지만 일반적인 최적화 문제는 아님
• 최종 문제는 $p^{HVAC}$ 로 표현되는 에너지 소비전력 최소화이고, 동시에 제약 조건 위반 횟수를 최소화하는 방향으로 조정하는 것임
• multi-objective, uncontrained minimization problem
  $$min_{\alpha \subset A} (p^{HVAC}(\alpha), f_{T_{SP}^{AL1}}(\alpha), f_{T_{constr}^{AL2}}(\alpha), f_{a_{fluct}}(\alpha))$$
  • $\alpha$ 는 reward tuning hyperparameter의 벡터(hyperparameters space의 element)
  • $p^{HVAC}(\alpha)$ 는 연간 HVAC 전력량
  • $f_{x}(\alpha)$ 는 1년간 제약조건 위반 혹은 바람직하지 않은 행동의 심각도 함수
  • 이 세 가지의 함수는 서로 다른 세 타입의 패널티에 기초함
• 이걸 정의하는 것에 집중하고, 하이퍼 파라미터 영역에서 sampling하는 것을 이후에 논의

제약 조건 위반 행렬

• 에이전트의 성능을 평가하기 위해서는 3가지 타입의 원하지 않는 타입의 심각도에 대해 알아야함

1. AL1 지점에서 설정값과의 편차
2. AL2 지점에서 온도 제약 조건 위반
3. action variables의 변동

• 이 각각의 효과의 심각도는 유클리드 거리 혹은 L2 norm으로 계산

$$||x||{2} = \sqrt{ \sum^{T}{t=1} x^{2}_{t} }$$

• $T$ = 일 년의 timestep 개수
• $x_{t}$ = 각각의 unwanted effect의 측정값
• 이 정규화는 작은 위반에도 패널티를 주면서, 큰 제약 조건 위반에 더 가중을 둠.
• $L_{2}$ norm 다음에 $L_{\infty}$ norm(연간 가장 큰 $x_{t}$)을 분석 목적으로 logging함
• 우선은 온도가 목표 지점보다 온도가 높을 때나 낮을 때나 $T^{AL1}$과 $T_{SP}^{AL1}$의 편차는 최소화되어야함
  $$f_{T_{SP}^{AL1}}(\alpha) = \sqrt{ \sum_{t=1}^{T}(T_{t}^{AL1} - T_{SP}^{AL1})^2 }$$
• $T_{constr}^{AL2}$의 위반 사항의 경우에는 $T^{AL2}$가 제약(constraint) 온도보다 얼마나 높은지만 고려되어야함
  $$f_{T_{constr}^{AL2}}(\alpha) = \sqrt{ \sum_{t=1}^{T}(max(0, T_{constr}^{AL2} - T_{t}^{AL2}))^2 }$$
• action의 변동에 관해서 agent는 큰, 고주파 oscillations을 가져서는 안됨. 그러므로 이전과 현재의 action 값의 차이를 반영
  $$f_{a_{fluct}}(\alpha) = \sqrt{ \sum_{t=1}^{T}(a_{t} - a_{t-1})^2}$$

sampler section

• Bayesian TPE Sampler를 사용
  • 보상함수의 hyperparameter space도 고차원이고 다중 목표 최적화에 있어서는 중간 결과 조정이 더 합리적
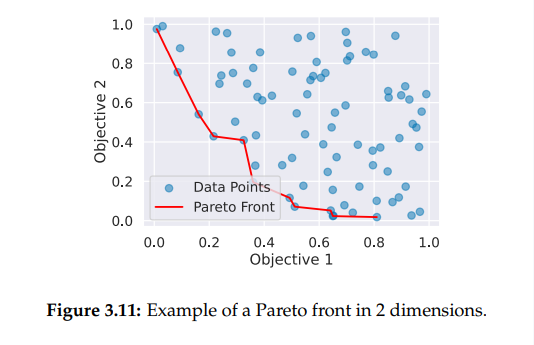
• sampler가 더 나은 보상으로 이끌기 위해 hyperparameter를 추출하는 단일 목표 최적화와는 다르게 다중 목표 TPE는 Pareto front라고 불리는 곳에서 hyperparameter를 추출하려고 한다
  • Pareto front(pareto frontier, pareto curve) : multi-objective optimization 기법. 최적의 설계해들은 곡선, 곡면, 초곡면 등을 이루게 되어 이를 파레토 최적해 표면이라고 부름
• 이 front는 모두 non-dominated solution으로 구성됨.
• 모든 최적화 metrics에서 첫 번째 구성을 능가는 다른 구성이 없는 방향으로 행동을 이끈다면 구성은 비 지배적이다.
  

Experiment outline

• reward tuning 실험의 목표는 4개의 성능 지표를 pareto front 형태로 만드는 것
• 이를 달성하기 위해서 agent는 서로 다른 하이퍼 파라미터 구성을 200회 학습함
• 이 구성들은 TPE Sampler로부터 추출됨
• 각각의 구성은 훈련 방해 데이터로 10 episode간 다시 학습하고 검증 방해 데이터로 평가됨
• 하이퍼 파라미터 튜닝 실험을 통해 찾은 알고리즘 하이퍼 파라미터는 모든 보상 구성에 사용됨
• 보상 튜닝 실험은 baseline conbbroller의 성능을 비교함