[라이트 딥러닝] n. Backpropagation 수식 풀이 및 검증

출처: https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/

A Step by Step Backpropagation Example

 

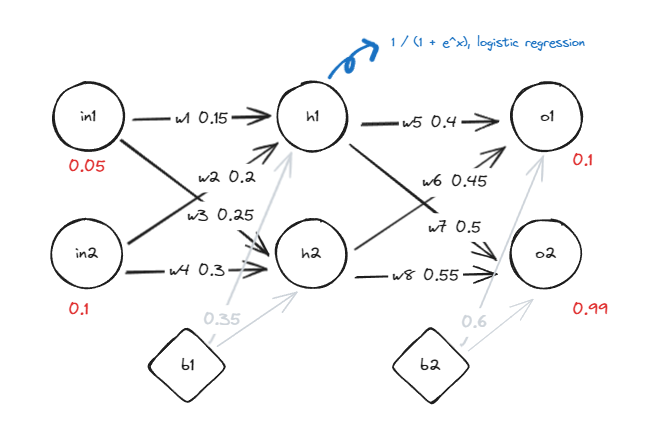
feed forward 계산

1. h1 구하기
$$net_{h1} = 0.05 * 0.15 + 0.1 * 0.2 + 0.35 = 0.3775$$
$$out_{h1} = \frac{1}{1 + e^{-0.3775}} = 0.5932699921071872$$

2. h2 구하기
$$net_{h2} = 0.05 * 0.25 + 0.1 * 0.3 + 0.35 = 0.39249999999999996$$
$$out_{h2} = \frac{1}{1+e^{-0.3925}} = 0.596884378259767$$

3. o1 구하기
$$net_{o1}= out_{h1}* 0.4 + out_{h2}* 0.45 + 0.6 = 1.10590596705977$$
$$out_{o1} = \frac{1}{1 + e^{-1.105906}} = 0.7513650695523157$$

4. o2 구하기
$$net_{o2}= out_{h1}* 0.5 + out_{h2}* 0.55 + 0.6 = 1.2249214040964653$$
$$out_{o2}= \frac{1}{1+e^{-1.224921}}=0.7729284653214625$$

5. error 구하기
여기에서는 squared error function을 사용함
$$E_{total}= \sum\limits \frac12(target - output)^{2}$$
$$E_{o1}= \frac 12 (0.01 - 0.7513650695523157)^{2}= 0.274811083176155$$
$$E_{o2}= \frac 12 (0.99 - 0.7729284653214625)^{2}= 0.023560025583847746$$
$$E_{total}= E_{o1}+ E_{o2} = 0.274811083176155 + 0.023560025583847746 = 0.2983711087600027$$

 

 

Back propagation

output layer backward pass

예제

• w5 업데이트를 위해서 w5에 대해 $E_{total}$ , 즉 cost를 편미분한 값이 필요함
• chain rule을 적용시켜보면

$$\frac{\partial E_{total}}{\partial w_{5}} = \frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial w_{5}}$$

 

1. $\frac{\partial E_{total}}{\partial out_{o1}}$

$$E_{total} = \frac12 (target_{o1} - out_{o1})^{2} + \frac12 (target_{o2} - out_{o2})^{2}$$
$$\frac{\partial E_{total}}{\partial out_{o1}} = 2 * \frac 12 (target_{o1} - out_{o1})^{2-1} * -1 + 0 \ = -target_{o1}+ out_{o1} = 0.7413650695523157$$

• 겉미분 결과 2, 속미분 결과 -1, 뒷항은 상수취급

 

2. $\frac{\partial out_{o1}}{\partial net_{o1}}$
   $$out_{o1}= \frac{1}{1+e^{-net_{o1}}}$$
   $$\frac{\partial out_{o1}}{\partial net_{o1}} = out_{o1}(1-out_{o1}) = 0.18681560180895948$$

• logistic function의 미분 공식에 의해 $f(x) = \frac{1}{1+e^{x}}$ 형태라면 $f'(x) = f(x)(1-f(x))$ 로 정의됨.

 

3. $\frac{\partial net_{o1}}{\partial w_{5}}$
   $$net_{o1}= w_{5} * out_{h1}+ w_{6}* out_{h2} + b_{2} * 1 = 0.5932699921071872$$
   $$\frac{\partial net_{o1}}{\partial w_{5}} = out_{h1}= $$
   
   
   
4. $\frac{\partial E_{total}}{\partial w_{5}}$
   $$\frac{\partial E_{total}}{\partial w_{5}} = 0.7413650695523157 * 0.18681560180895948 * 0.5932699921071872 = 0.08216704056423078$$
   
   
   
5. $w_{5}^{+}$ 업데이트
   $$w_{5}^{+} = w_{5}- lr * \frac{\partial E_{total}}{\partial w_{5}} = 0.4 - 0.5 * 0.08216704056423078 = 0.35891647971788465$$

• 위 과정을 요약하면 이런 식이 나온다.
  $$-(target_{o} -out_{o}) * out_{o}(1-out_{o}) * out_{h}$$

 

 

나머지 가중치 업데이트

$$\begin{matrix} w_{6}^{+} &=& 0.45 - 0.5 * (-0.01 + out_{o1}) * out_{o1}(1-out_{o1}) * out_{h2}
\\ &=& 0.45 - 0.5_(-0.01 + 0.7513650695523157) * 0.7513650695523157(1-0.7513650695523157) *0.596884378259767
\\ &=& 0.45 - 0.5 * 0.08266762784753325
\\ &=& 0.4086661860762334 \end{matrix}$$

 

$$\begin{matrix} w_{7}^{+} &=& 0.5 - 0.5 * (-0.99 + out_{o2}) * out_{o2}(1-out_{o2}) * out_{h1}
\\ &=& 0.5 - 0.5_(-0.99 + 0.7729284653214625) * 0.7729284653214625(1-0.7729284653214625) *0.5932699921071872
\\ &=& 0.5 - 0.5 * -0.02260254047747507
\\ &=& 0.5113012702387375 \end{matrix}$$

 

$$\begin{matrix} w_{8}^{+} &=& 0.55 - 0.5 * (-0.99 + out_{o2}) * out_{o2}(1-out_{o2}) * out_{h2}
\\ &=& 0.55 - 0.5_(-0.99 + 0.7729284653214625)* 0.7729284653214625(1-0.7729284653214625) *0.596884378259767
\\ &=& 0.55 - 0.5 * -0.022740242215978222
\\ &=& 0.5613701211079891 \end{matrix}$$

 

 

Hidden layer 계산

예제(w1)

 

$$\frac{\partial E_{total}}{\partial w_{1}}= \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$$

• 위 식을 구해야한다.
  $$E_{total}= E_{o1} + E_{o2}, \quad \therefore \frac{\partial E_{total}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial out_{h1}} + \frac{\partial E_{o2}}{\partial out_{h1}}$$
  $$\frac{\partial E_{o1}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}}$$

 

• 한 항씩 분해 - 1

$$\frac{\partial E_{o1}}{\partial net_{o1}} = \frac{\partial E_{o1}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}}$$

$$ \frac{\partial E_{o1}}{\partial out_{o1}} = 2 * \frac 12 (target_{o1} - out_{o1})^{2-1} * -1 + 0 \ = -target_{o1}+ out_{o1} = 0.7413650695523157$$

$$\frac{\partial out_{o1}}{\partial net_{o1}} = out_{o1}(1-out_{o1}) = 0.18681560180895948$$

$$\therefore \frac{\partial E_{o1}}{\partial net_{o1}} = \frac{\partial E_{o1}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} = 0.7413650695523157 * 0.18681560180895948 = 0.13849856162855698$$

 

• 한 항 씩 분해 - 2

$$\frac{\partial net_{o1}}{\partial out_{h1}} = w5$$ $$\begin{matrix} \because net_{o1} &=& w_{5} * out_{h1}+ w6 * out_{h2}+ b2*1
\ \frac{\partial net_{o1}}{\partial out_{h1}} &=& w_{5}\end{matrix}$$

 

• 결합

$$\frac{\partial E_{o1}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}} = 0.13849856162855698 * 0.4 = 0.05539942465142279$$

 

 

반대 항

$$\frac{\partial E_{o2}}{\partial out_{h1}} = \frac{\partial E_{o2}}{\partial net_{o2}} * \frac{\partial net_{o2}}{\partial out_{h1}}$$

 

• 한 항 씩 분해

$$\frac{\partial E_{o2}}{\partial net_{o2}} = \frac{\partial E_{o2}}{\partial out_{o2}} * \frac{\partial out_{o2}}{\partial net_{o2}}$$

$$ \begin{matrix} \frac{\partial E_{o2}}{\partial out_{o2}} &=& 2 * \frac 12 (target_{o2} - out_{o2})^{2-1} * -1 + 0 \\ &=& -target_{o2}+ out_{o2} = -0.99 + 0.7729284653214625 = -0.21707153467853746 \end{matrix} $$

 

$$\frac{\partial out_{o2}}{\partial net_{o2}} = out_{o2}(1-out_{o2}) = 0.17551005281727122$$

$$\begin{matrix} \frac{\partial E_{o2}}{\partial net_{o2}} &=& \frac{\partial E_{o2}}{\partial net_{o2}} * \frac{\partial net_{o2}}{\partial out_{h1}} \\ &=& -0.21707153467853746 * 0.17551005281727122 = -0.03809823651655623 \end{matrix}$$

 

• 한 항씩 분해 - 2

$$\frac{\partial net_{o2}}{\partial out_{h1}} = w_{7} = 0.5$$

 

• 결합

$$\begin{matrix} \frac{\partial E_{o2}}{\partial out_{h1}} &=& \frac{\partial E_{o2}}{\partial net_{o2}} * \frac{\partial net_{o2}}{\partial out_{h1}} \\ &=& -0.03809823651655623* 0.5 = -0.019049118258278114\end{matrix}$$

 

 

총 식

$$\frac{\partial E_{total}}{\partial w_{1}}= \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$$

$$\begin{matrix} \frac{\partial E_{total}}{\partial out_{h1}} &=& \frac{\partial E_{o1}}{\partial out_{h1}} + \frac{\partial E_{o2}}{\partial out_{h1}} \\ &=& 0.05539942465142279 + -0.019049118258278114 = 0.03635030639314468 \end{matrix}$$

$$\frac{\partial out_{h1}}{\partial net_{h1}} = out_{h1}(1-out_{h1}) = 0.24130070857232525$$

$$\begin{matrix} net_{h1} &=& input_{1}* w_{1}+ input_{2}* w_{3}+ b_{1}* 1
\ \frac{\partial net_{h1}}{\partial w_{1}} &=& input_{1} = 0.05\end{matrix} $$

 

• 정리하면

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{1}} &=& \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}
\\ & =& 0.03635030639314468 * 0.24130070857232525 * 0.05
\\ & = & 0.00043856773447434685\end{matrix}$$

$$w_{1}^{+}= w_{1}-lr * \frac{\partial E_{total}}{\partial w_1}$$

$$w_{1}^{+} = 0.15 - 0.5 * 0.00043856773447434685 = 0.1497807161327628$$

 

 

정리

$$\frac{\partial E_{total}}{\partial w_{1}}= \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$$

 

$$\frac{\partial E_{total}}{\partial w_{1}}= (\frac{\partial E_{o1}}{\partial out_{h1}} + \frac{\partial E_{o2}}{\partial out_{h1}}) * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$$

 

$$\frac{\partial E_{total}}{\partial w_{1}}=
{(\frac{\partial E_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}}) + (\frac{\partial E_{o2}}{\partial net_{o2}} * \frac{\partial net_{o2}}{\partial out_{h1}})} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$$

 

$$\frac{\partial E_{total}}{\partial w_{1}}=
{(\frac{\partial E_{o1}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}}) +
(\frac{\partial E_{o2}}{\partial out_{o2}} * \frac{\partial out_{o2}}{\partial net_{o2}} * \frac{\partial net_{o2}}{\partial out_{h1}})} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$$

 

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{1}} &=& (-target_{o1}+ out_{o1}) * \frac{\partial out_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}} \\ &+& (-target_{o2}+ out_{o2}) * \frac{\partial out_{o2}}{\partial net_{o2}} * \frac{\partial net_{o2}}{\partial out_{h1}} \\ & * & \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}} \end{matrix}$$

 

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{1}} &=& (-target_{o1}+ out_{o1}) * out_{o1}(1-out_{o1}) * \frac{\partial net_{o1}}{\partial out_{h1}} \\ &+&
(-target_{o2}+ out_{o2}) * out_{o2}(1-out_{o2}) * \frac{\partial net_{o2}}{\partial out_{h1}} \\
& * & \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}} \end{matrix}$$

 

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{1}} &=& (-target_{o1}+ out_{o1}) * out_{o1}(1-out_{o1}) * w_{5} \\ &+&
(-target_{o2}+ out_{o2}) * out_{o2}(1-out_{o2}) * w_{7} \\
& * & out_{h1}(1-out_{h1}) * \frac{\partial net_{h1}}{\partial w_{1}} \end{matrix}$$

 

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{1}} &=& (-target_{o1}+ out_{o1}) * out_{o1}(1-out_{o1}) * w_{5} \\ &+&
(-target_{o2}+ out_{o2}) * out_{o2}(1-out_{o2}) * w_{7} \\
& * & out_{h1}(1-out_{h1}) * \frac{\partial net_{h1}}{\partial w_{1}} \end{matrix}$$

 

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{1}} &=& (-target_{o1}+ out_{o1}) * out_{o1}(1-out_{o1}) * w_{5} \\ &+&
(-target_{o2}+ out_{o2}) * out_{o2}(1-out_{o2}) * w_{7} \\
& * & out_{h1}(1-out_{h1}) * input_{1} \end{matrix}$$

 

 

나머지

$w_{2}$

$$\frac{\partial E_{total}}{\partial w_{2}}= \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{2}}$$

 

• 위와 같으므로 $w_1$ 과 식은 같고 마지막 input만 다르게 곱해주면 된...다.

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{1}} &=& \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}
\\ & =& 0.03635030639314468 * 0.24130070857232525 * 0.1
\\ & = & 0.0008771354689486937\end{matrix}$$

 

$$w_{2}^{+} = w_{2} - lr * \frac{\partial E_{total}}{\partial w_{2}}$$
$$w_{2}^{+} = 0.2 - 0.5 * 0.0008771354689486937 = 0.19956143226552567$$

 

 

$w_{3}$

$$\frac{\partial E_{total}}{\partial w_{3}}= \frac{\partial E_{total}}{\partial out_{h2}} * \frac{\partial out_{h2}}{\partial net_{h2}} * \frac{\partial net_{h2}}{\partial w_{3}}$$

 

$$\frac{\partial E_{total}}{\partial w_{3}}= (\frac{\partial E_{o1}}{\partial out_{h2}} + \frac{\partial E_{o2}}{\partial out_{h2}}) * \frac{\partial out_{h2}}{\partial net_{h2}} * \frac{\partial net_{h2}}{\partial w_{3}}$$

 

$$\frac{\partial E_{total}}{\partial w_{3}}=
{(\frac{\partial E_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h2}}) + (\frac{\partial E_{o2}}{\partial net_{o2}} * \frac{\partial net_{o2}}{\partial out_{h2}})} * \frac{\partial out_{h2}}{\partial net_{h2}} * \frac{\partial net_{h2}}{\partial w_{1}}$$

 

$$\frac{\partial E_{total}}{\partial w_{3}}=
{(\frac{\partial E_{o1}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h2}}) +
(\frac{\partial E_{o2}}{\partial out_{o2}} * \frac{\partial out_{o2}}{\partial net_{o2}} * \frac{\partial net_{o2}}{\partial out_{h2}})} * \frac{\partial out_{h2}}{\partial net_{h2}} * \frac{\partial net_{h2}}{\partial w_{1}}$$

 

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{3}} &=& (-target_{o1}+ out_{o1}) * \frac{\partial out_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h2}} \\ &+&
(-target_{o2}+ out_{o2}) * \frac{\partial out_{o2}}{\partial net_{o2}} * \frac{\partial net_{o2}}{\partial out_{h2}} \\
&* & \frac{\partial out_{h2}}{\partial net_{h2}} * \frac{\partial net_{h2}}{\partial w_{3}} \end{matrix}$$

 

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{3}} &=& (-target_{o1}+ out_{o1}) * out_{o1}(1-out_{o1}) * \frac{\partial net_{o1}}{\partial out_{h2}} \\ &+&
(-target_{o2}+ out_{o2}) * out_{o2}(1-out_{o2}) * \frac{\partial net_{o2}}{\partial out_{h2}} \\
& * & \frac{\partial out_{h2}}{\partial net_{h2}} * \frac{\partial net_{h2}}{\partial w_{3}} \end{matrix}$$

 

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{3}} &=& (-target_{o1}+ out_{o1}) * out_{o1}(1-out_{o1}) * w_{6} \\ &+&
(-target_{o2}+ out_{o2}) * out_{o2}(1-out_{o2}) * w_{8} \\
& * & \frac{\partial out_{h2}}{\partial net_{h2}} * \frac{\partial net_{h2}}{\partial w_{3}} \end{matrix}$$

 

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{3}} &=& (-target_{o1}+ out_{o1}) * out_{o1}(1-out_{o1}) * w_{6} \\ &+&
(-target_{o2}+ out_{o2}) * out_{o2}(1-out_{o2}) * w_{8} \\
& * & out_{h2}(1-out_{h2}) * \frac{\partial net_{h2}}{\partial w_{3}} \end{matrix}$$

 

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{3}} &=& (-target_{o1}+ out_{o1}) * out_{o1}(1-out_{o1}) * w_{6} \\ &+&
(-target_{o2}+ out_{o2}) * out_{o2}(1-out_{o2}) * w_{8} \\
&*& out_{h2}(1-out_{h2}) * input_{1} \end{matrix}$$

 

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{3}} &=& (0.05475832085958778 + -0.020954030084105933) * 0.01203067086246092 = 0.0004066882960587459 \end{matrix}$$

 

$$w_{3}^{+} = w_{3}- lr * \frac{\partial E_{total}}{\partial w_{3}}$$

 

$$w_{3}^{+} = 0.25 - 0.5 * 0.0004066882960587459 = 0.24979665585197064$$

 

 

$w_{4}$

$$\frac{\partial E_{total}}{\partial w_{4}}= \frac{\partial E_{total}}{\partial out_{h2}} * \frac{\partial out_{h2}}{\partial net_{h2}} * \frac{\partial net_{h2}}{\partial w_{4}}$$

 

• 위와 같으므로 $w_3$ 과 식은 같고 마지막 input만 다르게 곱해주면 된...다.

$$\begin{matrix} \frac{\partial E_{total}}{\partial w_{4}} &=& \frac{\partial E_{total}}{\partial out_{h2}} * \frac{\partial out_{h2}}{\partial net_{h2}} * \frac{\partial net_{h2}}{\partial w_{4}}
\\ & =& 0.033804290775481846 * 0.2406134172492184 * 0.1
\\ & = & 0.0008133765921174917\end{matrix}$$

 

• 따라서 $w_{4}^{+}$ 는 아래와 같다.

$$w_{4}^{+} = w_{4}- lr * \frac{\partial E_{total}}{\partial w_{4}}$$

$$w_{3}^{+} = 0.3 - 0.5 * 0.0008133765921174917 = 0.29959331170394127$$

 

 

업데이트 후 성능개선확인

• 업데이트 된 값으로 다시 feed forwarding을 수행해서 차이를 보자.

 

feed forwarding

 

$$net_{h1}= 0.05 * 0.1498 + 0.1 * 0.1996 + 0.35 = 0.37744999999999995$$
$$out_{h1}= \frac{1}{1 + e^{-net_{h1}}} = 0.5932579270154956$$
$$net_{h2}= 0.05 * 0.2498 + 0.1 * 0.2996 + 0.35 = 0.39244999999999997$$
$$out_{h2}= \frac{1}{1 + e^{-net_{h2}}} = 0.5968723475306276$$

$$net_{o1}= out_{h1}* 0.03598 + out_{h2} * 0.4087 + 0.6 = 1.056861998441629$$
$$out_{o1} = \frac{1}{1 + e^{-net_{o1}}} = 0.7420904125813247$$
$$net_{o2}= out_{h1}* 0.5113 + out_{h2} * 0.5614 + 0.6 = 1.2384169139867174$$
$$out_{o2} = \frac{1}{1 + e^{-net_{o2}}} = 0.7752883350296511$$

 

cost 구하기

$$E_{total}= \sum\limits \frac12(target - output)^{2}$$
$$E_{o1} = \frac 12 (0.01 - 0.7420904125813247)^{2} = 0.2679781860967471$$
$$E_{o2} = \frac 12 (0.99 - 0.7752883350296511)^{2} = 0.02305054953716967$$
$$\therefore E_{total}= 0.2679781860967471 + 0.02305054953716967 = 0.2910287356339168$$

 

• 이전 cost와 비교해보면
  $$E_{prev} = 0.2983711087600027$$
  $$E_{total}= 0.2910287356339168$$
  $$E_{prev} - E_{total} = 0.007342373126085933$$

확실히 좋아졌음을 확인할 수 있다!